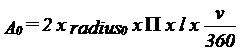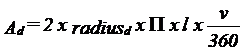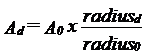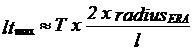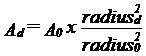|
RESEARCH DEVELOPMENT Kurt Grey Physiotherapist |
DYNAMIC FOCUSINGDistribution of energy during ultrasound treatment on curved surfaces |
|||||||||
|
Main Menu:
ULTRASOUND Research and Development:
Clinical guidance Tools and Tutorials:
MISCELLANEOUS:
LINKS Contact:
Downloads:
Latest update : 24-03-2011
|
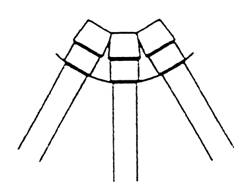
A) Convex: Sphere/cylinder B) Concave: sphere/cylinder
This figure demonstrates two positions of the transducer during treatment with its beam direction into the body: focused (A) and de-focused(B)
INTRODUCTIONThis report explains a hypothesis and its preliminary testing: Ultrasound treatment on the human body usually means, that the transducer is moved across the curves of the skin following the contours of the body, whether the target is the Achilles tendon, the quadriceps muscle, a shoulder tendon or any other structure. The body contour is either concave or convex (most common). The degree of curving (the body radius) varies between the body regions. In a convex region the beam is pointing towards the centre (or axis) of the body part. The buttock resembles a sphere, and the thigh a cylinder. The total area exposed to ultrasound decreases as the beam enters the tissue and at the centre (of the ”sphere”) an area no bigger than that of the beam (ERA) is exposed. The local exposure time increases accordingly. When treating a concave surface, the exposed area increases with tissue depth, and the local treatment time decreases consequently. The radius of the body contour and the tissue depth determine the effect.
A simple mathematical model is explained: ABSTRACTThe setting of the apparatus timer, the total treatment time (T) in ultrasound therapy is based on the local treatment time at the skin surface, lt0. The total time T is calculated as lt0xA0/ERA, where A0 is the area of the irradiated skin surface and ERA is the Effective Radiation Area, i.e. the transverse area of the ultrasound beam. The local treatment time, however, is only consistent throughout the tissue when treating flat surfaces. When moving the transducer across curved surfaces the irradiation time of deeper areas will increase under convex surfaces and decrease under concave surfaces. If this is ignored, then our ability to compare treatments is reduced. This article presents a simple model for the calculation of lt at any site. Presuming the surface has the shape of either a section of a cylinder or a sphere the area at different depths is found. Ad is the area at the depth "d". It is calculated by measuring r0 = radius at skin, d = distance from skin to tissue in question and A0, the exposed skin area.
The local treatment time in the injured tissue can now be chosen as part of a standard dosage by the therapist. T as well as the local treatment time throughout the tissue are derived from T = ltd x Ad / ERA.
To calculate Ad you need the tissue depth (d) and the radius (r) of the body contour. (The math implied is seen on the bottom of this page.) TABLESThe ratio between the surface area and the deep area can be read in the tables in the following links: NOTE. The exposed area cannot be smaller than that of the transducer( ERA,) e.g. 5 cm².
MEASURING RADIUSTools designed to measure the radius of the body contour (a radius-measurer or radius-meter) are found on the following links: radius meter 1 (for concave surfaces= fossae) radius meter 2 (for convex surfaces= thigh, buttock etc. Radius=0,5-7 cm) radius meter 3 ( same, 8-50 cm)
NOTE. Pay attention when scanning, printing and copying. The absolute measures can change in the process. Check out the control ruler (x- and y-lines, 10 cm) on the printed sheet. DO NOT use the option ”Fit to page” in Adobe!
Transfer the printed sheet to cardboard, an acrylic or wooden plate and carve out the tools. Put the tool up against the body contour, then turn it, and find which radius makes the best fit, and read the radius on the tool.
Mathematical modelsCYLINDERThe exposed area of the skin is a section of the cylinder (v):
and
A0 is the exposed area of the skin, Ad is the deep area in the tissue at d centimetres from the skin (concentric to the surface), radius0 is the distance from the centre of the cylinder to the skin, and radiusd is the distance from the centre to the tissue in question, l is the length of the exposed part of the cylinder, v/360 is the angular section of the cylinder, which is exposed. During palpation the injured tissue is defined and drawn on the skin surface, and thus the size of A0 is measured(7). It is assumed that the direction of the palpation is perpendicular to the skin surface.
The contour of the
body part, i.e. the curve of the surface can be expressed by its
radius. It may be measured by a
radius meter.
(The supplied drawings are printed and after checking out the
control measures, they are transferred to a piece of wood or plastic
and carved out carefully.) Put the edge of the tool on the skin
surface to be measured without pressing, and turn the tool until you
find the best fitting radius.
Radiusd is found by evaluating the distance (d) from the skin to the lesion :
The ratio between A(0) and A(d) (formula 1 and 2) shows that radius is the important parameter:
Which leads to :
If we study the local treatment time by using formula (5) from surface to centre, it becomes clear that Ad is diminished to zero, as we approach the centre. This would imply that lt(d) rises infinitely, which is obviously wrong. The model must be modified. The local treatment time, lt(d) cannot exceed the total treatment time, T. When a section of a cylinder is treated, the length of which is no longer than the beam diameter, the exposure time around the central part of the cylinder is T, actually within a central sphere with the diameter of ERA. The incident angle at the centre of the cylinder changes, though, according to the movement of the transducer along the skin surface. When the transducer is moved along the length (l) of the cylinder the maximum local treatment time lt(max) is calculated as :
The distribution of local treatment time along the path from surface to and across the centre show typical patterns, significantly different for convex and concave body contours. Fig 5 shows these typical distributions. The convex surface yields an increase until T is reached around the centre of the body part, where the lt – curve is flat. Having passed the central region it decreases again. The typical pattern of lt -distribution beneath concave body contours is one of decrease only. SPHEREOften, the body is curved along two axes. Several body parts are similar to a sphere. This created an even more marked impact on the local treatment time. The surface area of the sphere is calculated as 4 x PI x radius x radius, i.e. the areas of concentric spheres are related by the square of their radius:
and
This implies that
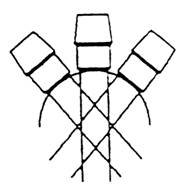
The local treatment time, lt, as calculated above is limited in the central region of a body part. Within a radius = radiusERA in convex spherical shapes the local treatment reaches its maximum = the total treatment time T. Even though the transducer is moved, and the direction of the beam changes due to this movement, the central tissue is still constantly exposed, as suggested in the illustration at the top of this page.
EXPERIMENTSPreliminary experiments with dynamic focusing in a setting with a moving light source (fig A1-3) and a computer simulation (fig A4-5) are demonstrated in the Gallery. In fig A1-3 a lamp was moved in three different patterns (1-3), thereby simulating exposure of the concave, the convex and the plane surface . The light was reflected from a white canvas, with the lamp at its upper edge. In each setting the moving light was captured by a camera with the shutter open for 3o seconds, i.e. during the entire exposure. The difference is obvious showing a spreading (1), a concentration (2) and an even distribution (3). A computer simulation of an exposure along a convex surface (A4-5) showed a similiar distribution. A lighter shade of grey indicates a longer exposure. The local summarized exposure time increased away from the surface and reached its maximum at the centre of the "limb". Experiments with dynamic focusing of ultrasound are being planned.
- o -
|